Lesson on: 18 April 2020
Worksheet: P6 Circles 2 (No. of revolutions) +
P6 Speed 1 (click on Speed topic)
|
Q13
- What does a complete revolution means? - What has it got to do with the Circumference of a circle? Tips: When you roll a coin on a flat surface, the distance travelled by the coin is the AREA of the coin or the CIRCUMFERENCE of the coin? ;p - How do we measure the distance of a circumference of a circle? Watch the animation video and the above questions will be answered! :) After watching the video, do Q13 and try Q14! | ||
|
Q15
Need more examples before trying Q14? Watch this video then! | ||
|
Q16
Let's watch this video to learn how to work backward to find the number of revolutions! ;p Do Q17! | ||
|
Putting on Your Thinking Cap! (Q18)
Is coming to the end of Circles topic! You want to challenge yourself by working on last question? ;p Tips: For the area of small square, we need to rotate it! How? Hmmmm....for you to think out of the Box! :) Try it before watching the video ya! :) | ||
End of Lesson!
Lesson on: 11 April 2020
Worksheet: P6 Circles 2
Dear Parents,
Below is the worksheet (Circles 2) for the lesson on 11 April 2020 (Sat).
Below is the worksheet (Circles 2) for the lesson on 11 April 2020 (Sat).
| p6_circle_2__cut_paste_online_student.pdf |
Videos for Worksheet questions
Instructions:
1) Except for the questions in the videos (Q3b-> Listen to the hint, Q3c, Q4b to Q4e, Q6, Q9 and Q12, student is to do the rest of the questions except Q13 to Q17, as homework.
2) It is recommended that the student watches the videos FIRST before attempting the questions. Student should recap what was taught instead of just copying the working from the videos.
3) Student is to complete the homework and 'hand in' as soon as possible so that we can have the Zoom consultation (if needed) to go through the homework questions before the next lesson. Student who hand in their homework after Thursday will have their Zoom consultation on the following week.
4) Parent is to schedule with the Tutor, a convenient time (morning slots are available now except Monday & Saturday, since Full HBL in school w.e.f. 4 May 2020!) for the Zoom consultation to go through homework questions. The duration ranges from 40 min to 1 hour, depends on the number of questions to go through with your child that he/she does not know.
Note: Your child's workings (saved in pdf format) are to be submitted to the Tutor ONE DAY BEFORE the Zoom consultation.
1) Except for the questions in the videos (Q3b-> Listen to the hint, Q3c, Q4b to Q4e, Q6, Q9 and Q12, student is to do the rest of the questions except Q13 to Q17, as homework.
2) It is recommended that the student watches the videos FIRST before attempting the questions. Student should recap what was taught instead of just copying the working from the videos.
3) Student is to complete the homework and 'hand in' as soon as possible so that we can have the Zoom consultation (if needed) to go through the homework questions before the next lesson. Student who hand in their homework after Thursday will have their Zoom consultation on the following week.
4) Parent is to schedule with the Tutor, a convenient time (morning slots are available now except Monday & Saturday, since Full HBL in school w.e.f. 4 May 2020!) for the Zoom consultation to go through homework questions. The duration ranges from 40 min to 1 hour, depends on the number of questions to go through with your child that he/she does not know.
Note: Your child's workings (saved in pdf format) are to be submitted to the Tutor ONE DAY BEFORE the Zoom consultation.
|
Learn the areas of 2 more shapes that are commonly seen in Circle questions! They are Area of Boomerang and Area of Half-leaf!
If you have learnt on these 2 shapes in school, you may skip this video :) | ||
|
Q3c & Q3b
Let's learn how to see Area of Half-leaf (Q3c) and Area of Boomerang (Q3b -> Only hints are given) in Circle questions! DO Q3a, Q3b and Q3d as homework! | ||
Cut & Paste techniques!!!
Let's see how we can use Cut & Paste techniques to solve Circles questions! :) Let's open our MIND and see the MAGIC ya!
Let's start with the basics by looking at Q4b to Q4e! After watching the videos, you SHOULD be able to do Q4a by yourself! :)
Let's see how we can use Cut & Paste techniques to solve Circles questions! :) Let's open our MIND and see the MAGIC ya!
Let's start with the basics by looking at Q4b to Q4e! After watching the videos, you SHOULD be able to do Q4a by yourself! :)
|
But before we start, who can you see in the picture on the right?
A young lady or an old lady? ;p Well ...it is just HOW your eyes want you to SEE! Both ladies are actually IN the pic! Can you see them? |
Optical Illusion
|
|
|
|
| ||||||||
|
Q6
See how to find the sum of Circumferences of circles WITHOUT having the diameter of each circle! | ||
|
Q9
After watching this video, you should be able to solve Q5, Q7, Q8, Q10 & Q11) better. Do remember to apply what you have learnt so far like: - Area of New shapes (Boomerang and half-leaf) learnt! - For perimeter-> outline with highlighter. Tick by checking the outlined lines. -To insert the correct fraction IN FRONT of the formula for the shape e.g. 1/4 for quadrant, 1/2 for semicircle, etc. - Cut & Paste techniques. - Use the correct pi as stated in the question. - Do NOT ASSUME the shape. Read the question for clues. Dare to accept the challenge? Try Q12 before listening to the video below! | ||
|
Q12
Did you get the answer as 138.51 cm2? If yes, GREAT JOB! CONGRATULATIONS! If you want to hear my applause to you, watch the video! :) If no, never mind! It is not an easy question. We learn along our way ya ;p So, watch the video and learn. FOr those who try, you see if you can be your OWN TEACHER and spot your mistakes?! If no... send your working to me and I will check for you! :) | ||
Next Lesson: 18 Apr 2020
- Circles 2 (No. of revolutions)
- Speed 1 (Basics)
- Speed 1 (Basics)
Lesson on: 4 April 2020
Worksheet: P6 Circles 1
Dear Parents,
Below is the worksheet (Circles 1) for the lesson on 4 April 2020 (Sat).
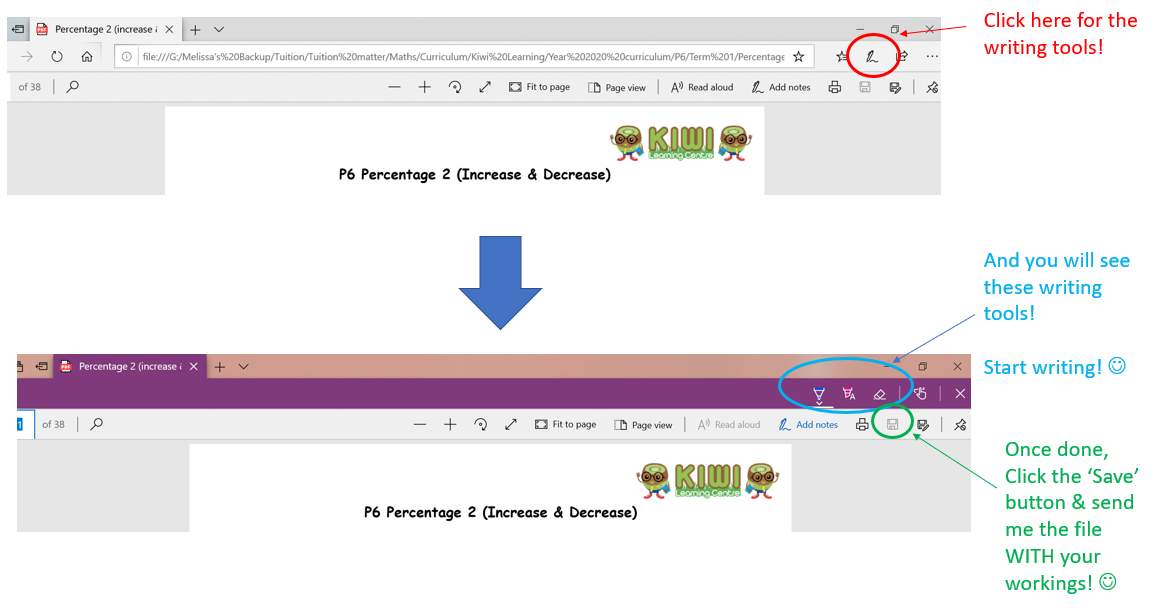
You may choose to download it and ask your child to do his/her workings using the writing tool found in pdf (see pic below for guidance). Alternatively, you can print out the worksheet and get your child to do on the hard copy. However, I need your assistance to scan your child's workings using an app called CamScanner (you can download from Play Store) and send to me those pics in pdf format, ONE DAY BEFORE the Zoom meeting. :)
Homework submission (Percentage 3) for Lesson on 28 Mar 2020:
Please scan your child's working and send to me in pdf format for my marking. I will send you back the file with my comments on it. Should your child need further explanation from me, feel free to arrange ANOTHER Zoom session with me. :)
Time slots for *Zoom session(s) are as follows:
P.S: I will increase the number of time slots as long as I am available ya! Fighting! :)
Tues: 3pm to 5pm
Wed: 10 am to 12pm (in view that it is school's E-learning Day w.e.f. Apr 2020)
Or 3pm to 8pm
Sun: 9am to 12pm Or 5pm to 8pm
*Zoom session may not be on 1 to 1 basis (subject to availability).
Below is the worksheet (Circles 1) for the lesson on 4 April 2020 (Sat).
You may choose to download it and ask your child to do his/her workings using the writing tool found in pdf (see pic below for guidance). Alternatively, you can print out the worksheet and get your child to do on the hard copy. However, I need your assistance to scan your child's workings using an app called CamScanner (you can download from Play Store) and send to me those pics in pdf format, ONE DAY BEFORE the Zoom meeting. :)
Homework submission (Percentage 3) for Lesson on 28 Mar 2020:
Please scan your child's working and send to me in pdf format for my marking. I will send you back the file with my comments on it. Should your child need further explanation from me, feel free to arrange ANOTHER Zoom session with me. :)
Time slots for *Zoom session(s) are as follows:
P.S: I will increase the number of time slots as long as I am available ya! Fighting! :)
Tues: 3pm to 5pm
Wed: 10 am to 12pm (in view that it is school's E-learning Day w.e.f. Apr 2020)
Or 3pm to 8pm
Sun: 9am to 12pm Or 5pm to 8pm
*Zoom session may not be on 1 to 1 basis (subject to availability).
| p6_circle_1_studentonline.pdf |
|
Where are the Writing tools in pdf?
Check it out here! :) |
Videos
Instructions:
1) Except for the questions in the videos (Q2c, Q3c, Q3e, Q5, Q7, Q8 and Challenge Round qn), student is to do the rest of the questions as homework.
2) Student who already knows the rudiments of a Circle WELL can proceed to attempt the questions first before checking the answers in the videos. If not, starting from Q3, it is recommended that the student watches the videos FIRST before attempting the questions. Student should recap what was taught instead of just copying the working from the videos.
3) Parent is to schedule with the Tutor, a convenient time for the Zoom session to go through homework questions. The duration ranges from 40 min to 1 hour, depends on the number of questions to go through with your child that he/she does not know. The session may not be on 1 to 1 basis.
Note: Your child's workings (saved in pdf format) are to be submitted to the Tutor ONE DAY BEFORE the Zoom session.
1) Except for the questions in the videos (Q2c, Q3c, Q3e, Q5, Q7, Q8 and Challenge Round qn), student is to do the rest of the questions as homework.
2) Student who already knows the rudiments of a Circle WELL can proceed to attempt the questions first before checking the answers in the videos. If not, starting from Q3, it is recommended that the student watches the videos FIRST before attempting the questions. Student should recap what was taught instead of just copying the working from the videos.
3) Parent is to schedule with the Tutor, a convenient time for the Zoom session to go through homework questions. The duration ranges from 40 min to 1 hour, depends on the number of questions to go through with your child that he/she does not know. The session may not be on 1 to 1 basis.
Note: Your child's workings (saved in pdf format) are to be submitted to the Tutor ONE DAY BEFORE the Zoom session.
Let's get started!
Tired of listening to my voice? ;p Well ... I have enclosed the following useful videos for you to learn more about Circles! Do watch them ya as these explanations will NOT be in my videos! :)
Why do we learn Circles?
|
|
Well ... there are so many things around you that are made of the shape of a circle! Look around! Can see some of them??! Give me some examples when I see you to claim for your stars! :)
You may grow up to become an architect or product designer which needs the shape of a circle! That is the reason why you need to learn how to calculate the area and circumference of a circle! Just like how you were taught to find the area and perimeter of a square, rectangle and triangle in P4 & P5! :) |
|
|
Pi can be expressed in 4 forms even though point (b), (c) and (d) are not mentioned in the video:
a) as decimal, i.e. 3.14 b) as fraction, i.e. 22/7 c) as calculator pi d) leave in terms of pi |
|
|
|
|
|
Have a break!
Let's hear a song about Circles, Radius, Diameter, Pi, circumference and area of a circle! Hope you like it! :) |
After watching videos, you can proceed to try out all the Q1 questions! :)
Let's get into the lesson!
|
Watch this video for the answers for the Pop Quiz questions in Page 1 and Page 5.
| ||
|
Q2c)
If you have gotten the following answers for this qn, you may skip this video and proceed to work on Q2a, Q2b & Q2d. Pls take note of the instruction to use for the pi for EACH QUESTION. Answers: Shape: 3/4 of a circle Circumference: 12pi cm Perimeter: (12pi + 16) cm Area: 48pi cm2 | ||
|
After watching this video, do Q3a & Q3b as hw.
| ||
|
After watching this video, do Q3d as hw.
| ||
|
You can try Q4 & Q6 first OR try these 2 questions AFTER you have watched this video!
For Q5, you will also learn how to solve a circle question when using the calculator value of pi! - How do you write it? - Do you round your answer off at EACH number statement? | ||
|
More than meets its eye!
We know that the fraction for a quadrant is 1/4. But where did it come from? Purely from the shape?! DO you know it can also come from ... Watch the video to find it out! ;p | ||
|
Dare the challenge! Try out Q8 first and see if you have gotten the following answers! If you do, WELL DONE! KEEP UP THE GOOD WORK! :)
Answers: a) 629 cm2 b) 118 cm | ||
|
Challenge Round (Optional)
If you want to learn more, try out this question first! Stuck?! Watch this video to solve the mystery! :) | ||
Next lesson
- Circle 2 (Composite figures involving 'Cut & Paste' + No. of revolutions)