Getting the concepts RIGHT at P5 level is very important so that your child is able to cope with new challenging questions when he is in P6! 😊
If your child is learning ANGLES right now in school... this is the right time to do
MIND-MAPPING (using one A3 paper or you can join two A4 papers to form one A3 paper!) with your child to map out the different types of properties of angles that he is learning RIGHT NOW! Draw figures if needed and beatify the map by using different colours of highlighters or colour pencils to make it less boring!!!
If your child is learning ANGLES right now in school... this is the right time to do
MIND-MAPPING (using one A3 paper or you can join two A4 papers to form one A3 paper!) with your child to map out the different types of properties of angles that he is learning RIGHT NOW! Draw figures if needed and beatify the map by using different colours of highlighters or colour pencils to make it less boring!!!
FYI, when comes to P6, there will be no more new properties of angles to be learnt. Students are to recapitulate the properties of angles of what they have learnt in P5 and find unknown angles in a complicated composite figure, i.e. figure that can be made up of more than 1 four-sided figure and a triangle! Hence, your child can re-use the mind-mapping map that he has created for P6 questions!!! 😊
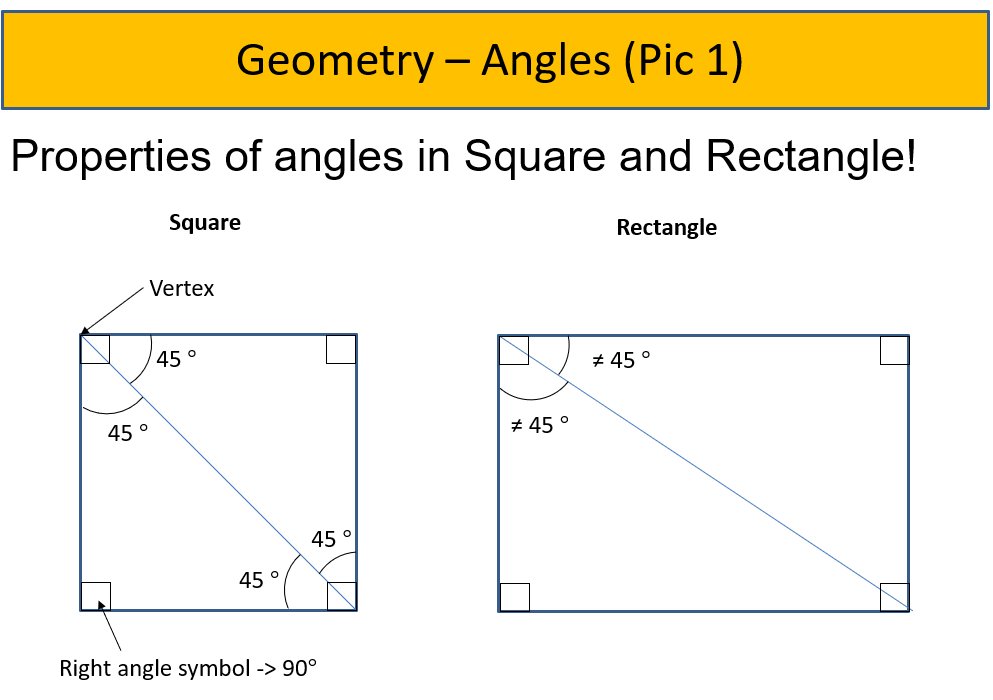
Angles is a heavy topic for P5 students as out of sudden, students are to learn so many different types of properties of angles as compared to P4 level where they only learn about the properties of angles for Square and Rectangle. So, what are those properties of angles found in Square and Rectangle?
Let’s recap, they are:
Angles is a heavy topic for P5 students as out of sudden, students are to learn so many different types of properties of angles as compared to P4 level where they only learn about the properties of angles for Square and Rectangle. So, what are those properties of angles found in Square and Rectangle?
Let’s recap, they are:
- All corner angle is 90 degrees.
- Each diagonal line (cut from 1 vertex to the opposite vertex) in a square cut each angle into 2 equal parts, i.e. each equal angle is 45 degrees. However, this is NOT true for Rectangle (see Pic 1).
In P5, what types of properties of angles will your child be learning?
They are:
They are:
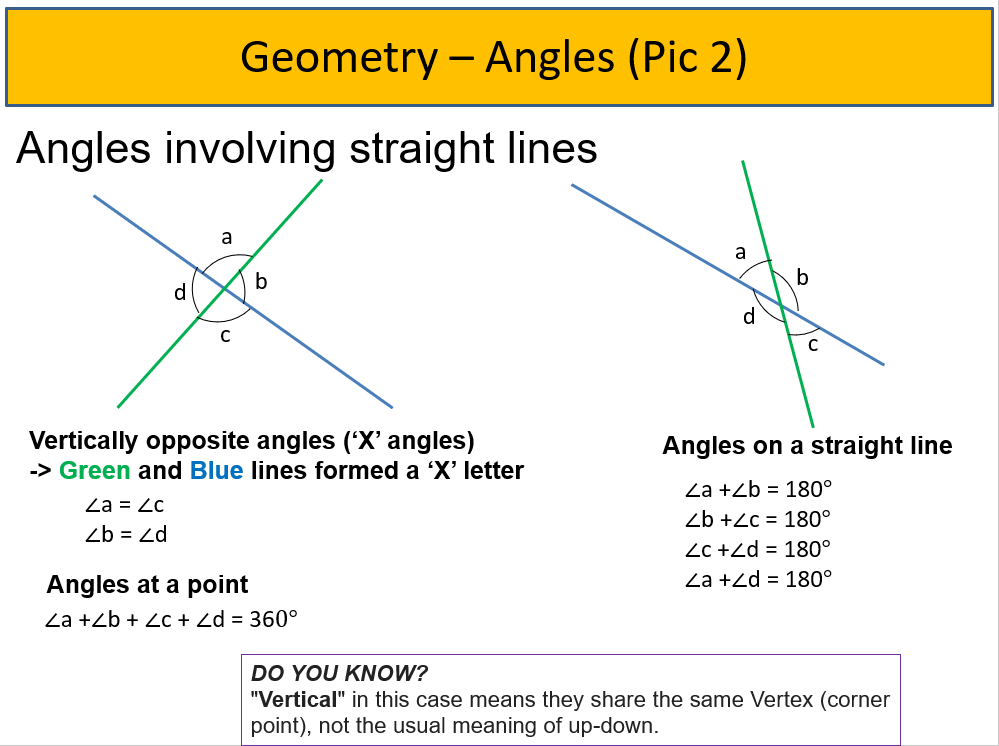
- Angles involving straight lines (See Pic 2):
- Angles on a straight line, i.e. all angles on one side of a straight line add up to 180 degrees.
- Angles at a point, i.e. all angles at a point add up to 360 degrees.
- Vertically opposite angles, i.e. angles opposite each other when two lines cross are equal to one another (or what we called it the ‘X’ angle)
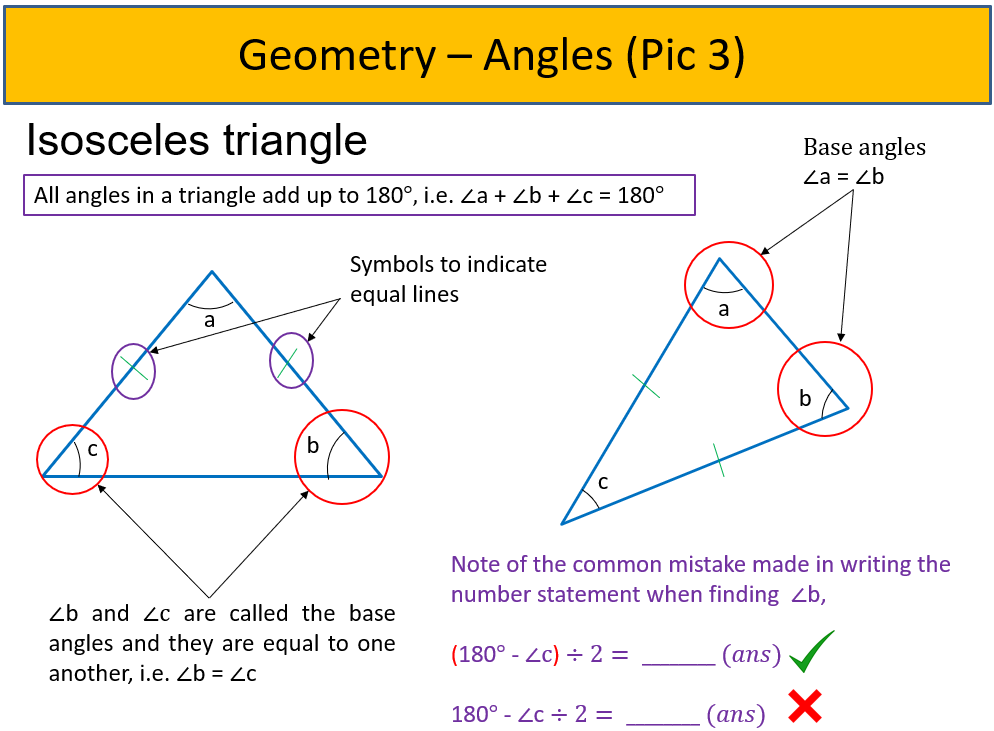
- Angles found in Triangles
- Sum of angles in a triangle add up to 180 degrees.
- Equilateral triangle (All sides are equal hence EACH angle is 60 degrees).
- Isosceles triangle (2 sides are equal hence the 2 angles [also called the ‘base angles’] where the two equal sides are, are equal to one another) (See Pic 3). Does your child know how to identify the 2 base angles? Give your child some isosceles triangles and see if he can identify the base angles correctly 😊
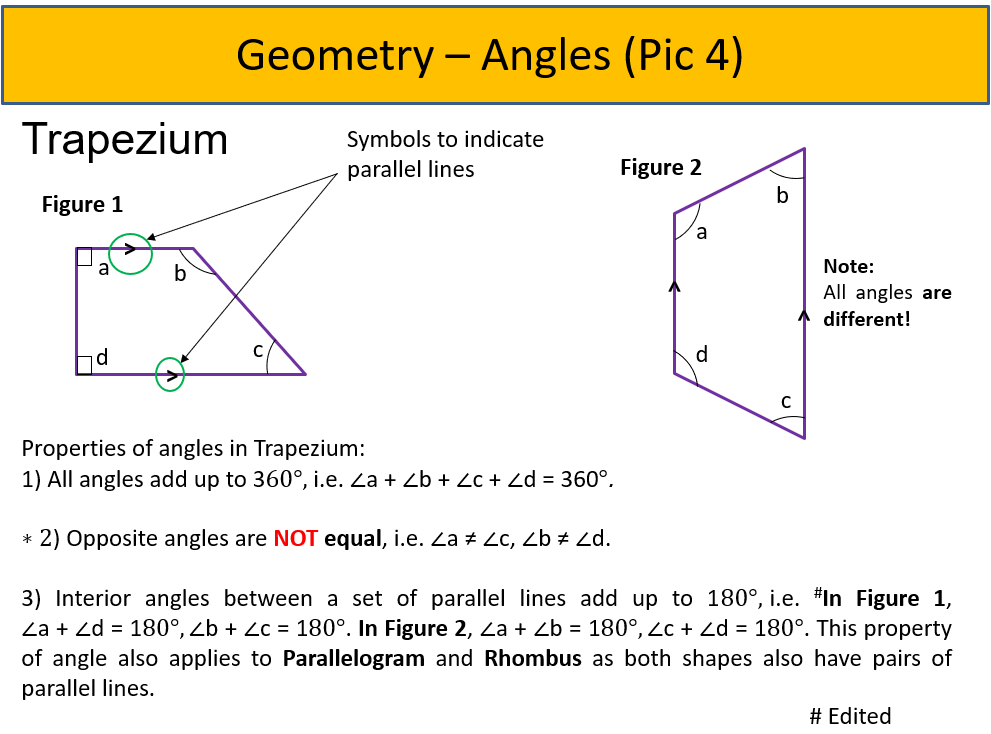
- Angles found in 4-sided figures
1) Trapezium (See Pic 4)
Note: Most students are mixed up the properties of angles for this shape with the other 2 4-sided figures. So, go through the properties for this shape FIRST!
- 1 pair of parallel lines
- All sides are NOT equal hence 2 opposite angles are NOT equal!
- All angles are different unless one of the angles is 90 degrees (See Figure 1) unlike Figure 2 where all angles are different.
- Interior angles between a set of parallel lines add up to 180 degrees (aka the ‘U’ or ‘C’ angle -> see below under ‘BONUS’ for more explanation).
- All angles add up to 360 degrees.
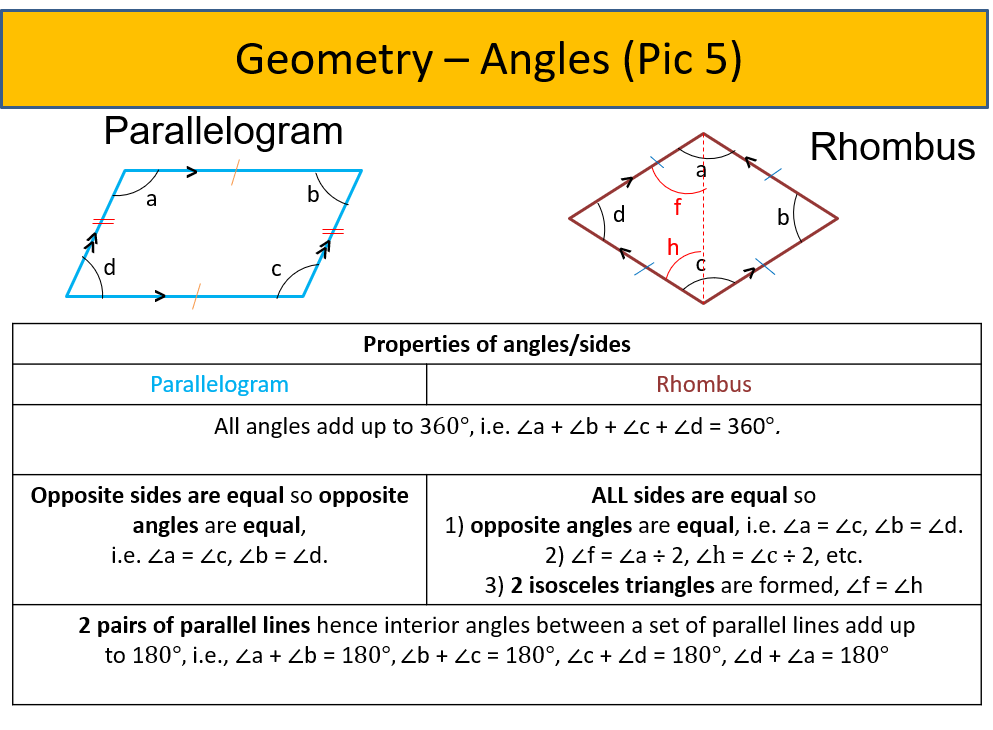
2) Parallelogram (See Pic 5)
- 2 pairs of parallel lines.
- 2 opposite sides are equal hence 2 opposite angles are equal!
- Interior angles between a set of parallel lines add up to 180 degrees (aka the ‘U’ or ‘C’ angle).
- All angles add up to 360 degrees.
3) Rhombus (See Pic 5)
- 2 pairs of parallel lines.
- All sides are equal hence 2 isosceles triangles will be formed when a diagonal line is cut across from 2 opposite vertices. The diagonal line cut each angle into 2 equal parts.
- Opposite angles are equal.
- Interior angles between a set of parallel lines add up to 180 degrees (aka the ‘U’ or ‘C’ angle).
- All angles add up to 360 degrees.
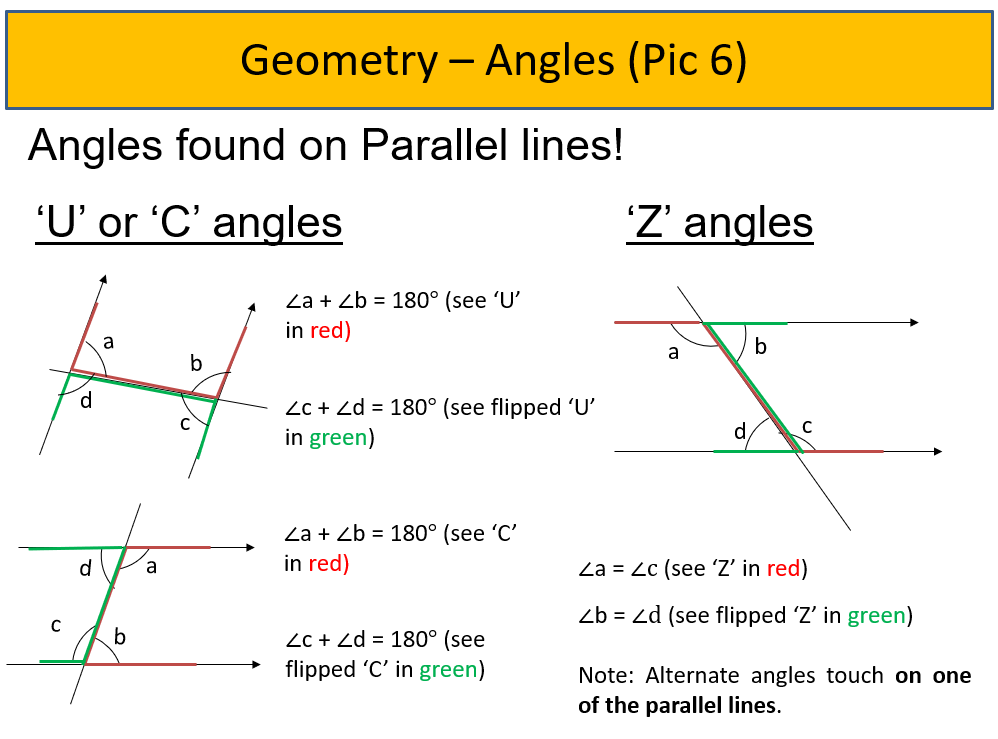
BONUS!!!
The following 2 properties of angles (see Pic 6) are angles that are GOOD to know!!! They can be found ONLY on PARALLEL LINES!! They are:
The following 2 properties of angles (see Pic 6) are angles that are GOOD to know!!! They can be found ONLY on PARALLEL LINES!! They are:
- Interior angles, i.e. Interior angles between a set of parallel lines add up to 180 degrees. Some schools called it the ‘U’ or ‘C’ angles as it looks like the said letter!
- Alternate angles (also called it the ‘Z’ angle as it looks like the said letter!)
Can the above 2 angles be found in parallelogram, rhombus and trapezium?
Answer:
Of course,yes!! Just draw a line between the 2 parallel lines and you will see the Z angles and more U angles appearing!😁
Small tips that will help your child to find the unknown angles much easier as well as identifying the next property of angles to apply! 😊
1) Mark out the shapes (e.g. rhombus, parallelogram) or ‘letters’ of property of angles (e.g. 'U' angle or 'Z' angle) that can be seen in the figure with different colours of highlighters.
2) Mark out ALL EQUAL lengths for square, rhombus and any straight lines that stated in the questions which are equal to one another e.g. PQ = QR. By doing so, you will see isosceles and/or equilateral triangles magically appear! :)
3) Put in the symbols for parallel lines in the figure! This will help you to see where are the 'U' or 'Z' angles! :)
4) Always write the angles that your child has found into the figure especially if your child has the habit of NOT writing any angle referencing in the number statements! ;p
5) Do NOT make ASSUMPTION! i.e. do NOT estimate the angles! Look out for clues to support your reasoning!
Do NOT measure the angles with a protractor UNLESS instruction given in the question, i.e. you see the word 'MEASURE' in the question.
6) Still stuck? Read the question carefully! The information and angles given in the question are CLUES! Your child must also learn to look at a BIGGER PICTURE! i.e. there might be a BIGGER triangle inside the two small triangles? or a small triangle inside a big triangle! ;p
Hope the above information is useful to your child's learning of angles and has made the topic of Angles much easier to understand! 😊 Get ready all the pens, highlighters or colour pencils and ask your child to work on the mind-mapping for ANGLES NOW!!! 😃
Answer:
Of course,yes!! Just draw a line between the 2 parallel lines and you will see the Z angles and more U angles appearing!😁
Small tips that will help your child to find the unknown angles much easier as well as identifying the next property of angles to apply! 😊
1) Mark out the shapes (e.g. rhombus, parallelogram) or ‘letters’ of property of angles (e.g. 'U' angle or 'Z' angle) that can be seen in the figure with different colours of highlighters.
2) Mark out ALL EQUAL lengths for square, rhombus and any straight lines that stated in the questions which are equal to one another e.g. PQ = QR. By doing so, you will see isosceles and/or equilateral triangles magically appear! :)
3) Put in the symbols for parallel lines in the figure! This will help you to see where are the 'U' or 'Z' angles! :)
4) Always write the angles that your child has found into the figure especially if your child has the habit of NOT writing any angle referencing in the number statements! ;p
5) Do NOT make ASSUMPTION! i.e. do NOT estimate the angles! Look out for clues to support your reasoning!
Do NOT measure the angles with a protractor UNLESS instruction given in the question, i.e. you see the word 'MEASURE' in the question.
6) Still stuck? Read the question carefully! The information and angles given in the question are CLUES! Your child must also learn to look at a BIGGER PICTURE! i.e. there might be a BIGGER triangle inside the two small triangles? or a small triangle inside a big triangle! ;p
Hope the above information is useful to your child's learning of angles and has made the topic of Angles much easier to understand! 😊 Get ready all the pens, highlighters or colour pencils and ask your child to work on the mind-mapping for ANGLES NOW!!! 😃